Appendix

Occlusion-compatible scanning-order

The following summary presents only a concept which could not be fully verified at the time of writing the thesis.

Consider two 3D scene points \(\boldsymbol{P}_1\) and \(\boldsymbol{P}_2\), which are projected onto a target image (virtual view) at the same pixel position \(p\), and onto the reference view at pixel positions \(\boldsymbol{p}_1'\) and \(\boldsymbol{p}_2'\) (see Figure 4.8). To perform an occlusion-compatible scanning order of the reference image, it is necessary to scan first the background point \(\boldsymbol{P}_1\) and then the foreground \(\boldsymbol{P}_2\). Hence, when projecting the 3D points \(\boldsymbol{P}_1\) and \(\boldsymbol{P}_2\) onto the reference view, it can be derived that \[|\boldsymbol{M}'\boldsymbol{P}_2-\boldsymbol{M'C}|<|\boldsymbol{M}'\boldsymbol{P}_1-\boldsymbol{M'C}|, (A.1)\] which is equivalent to the same inequality using pixels in the reference image, thus \[|\lambda_2'\boldsymbol{p}_2'-\lambda_e' \boldsymbol{e'}|<|\lambda_1'\boldsymbol{p}_1'-\lambda_e' \boldsymbol{e}'|, (A.2) \label{eq:distance2}\] where \(\boldsymbol{e'}\) corresponds to the epipole in the reference view. The points \(\boldsymbol{p}_1'\) and \(\boldsymbol{p}_2'\) are the projections of the background and foreground 3D points, respectively. Points \(\boldsymbol{p}_1'\) and \(\boldsymbol{p}_2'\) are therefore background and foreground pixels. By normalizing/dividing Equation ([eq:distance2]) with the homogeneous scaling factor \(\lambda_e'\), two cases can be distinguished. First, assuming \(\lambda_e'>0\), to perform the warping of background pixels \(\boldsymbol{p}_1\) prior to foreground pixels \(\boldsymbol{p}_2\), it is sufficient to scan the reference image from the border of the image towards the epipole \(e'\). Second, in the case \(\lambda_e'<0\), the reference image should be scanned from the epipole towards the borders of the image.

Test sequences and images

“Breakdancers” and “Ballet”

Figure A.1 and Figure A.2 illustrate the multi-view sequences “Breakdancers” and “Ballet”, respectively. These test sequences were acquired by Microsoft Research [111]. Table A.1 and Table A.2 provide the camera calibration parameters. The resolution of both sequences is \(1024 \times 768\) pixels and the frame rate is 15 frames per second. The calibration parameters were converted into a right-handed coordinate system with the origin of the image located at the top left of the image (see Section 2.2.3).

Figure A.1 Camera 3 of the sequence “Breakdancers”.

Figure A.2 Camera 3 of the sequence “Ballet”.

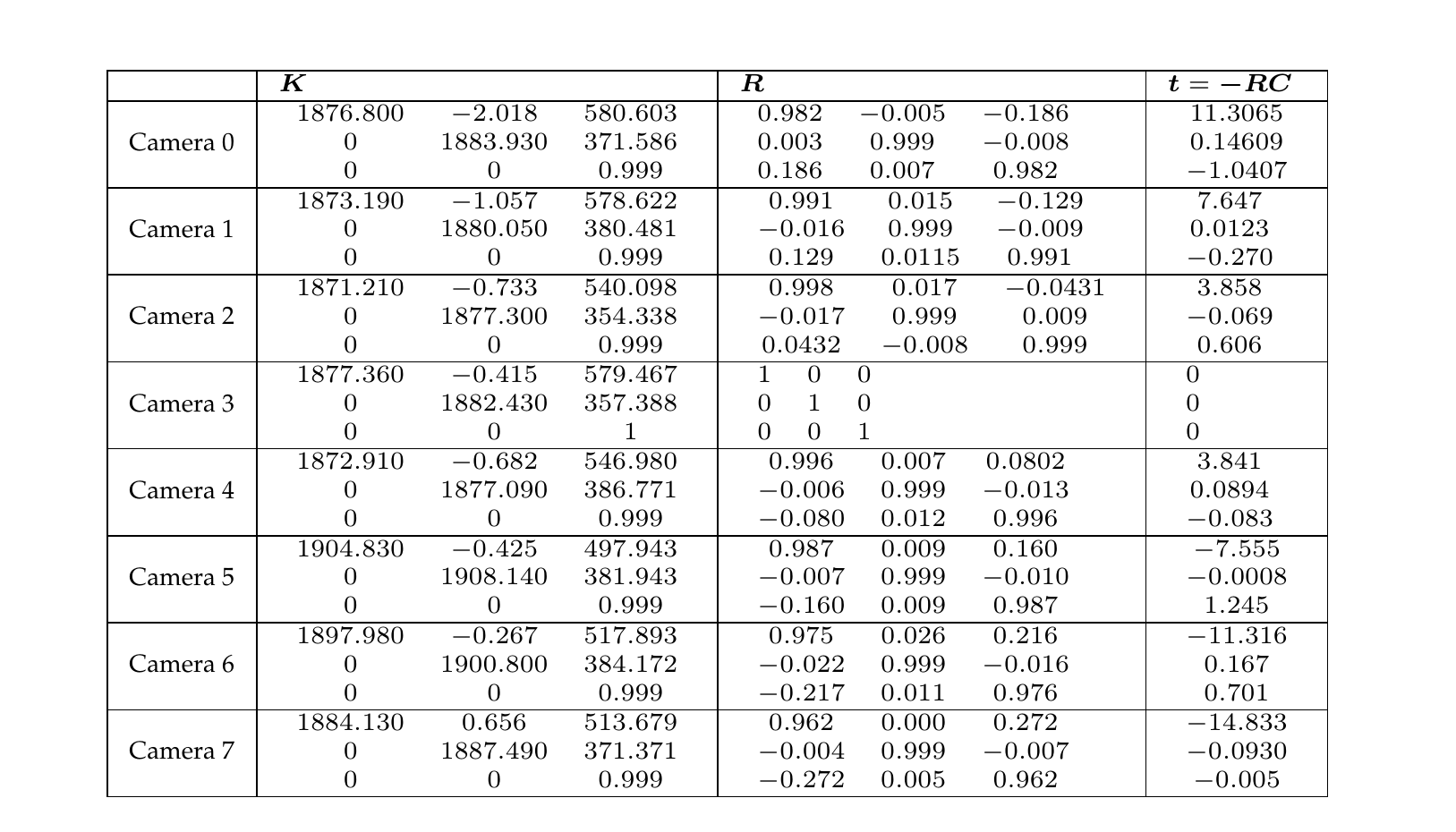
Table A.1 Calibration parameters of the multi-view sequence “Breakdancers”.

Table A.2Calibration parameters of the multi-view sequence “Ballet”.

“Livingroom”

Figure [figure:Livingroom] illustrates the multi-view images “Livingroom” and Table A.3 provides the camera calibration parameters. The data set was acquired and calibrated by the author. The acquisition of the images was performed using a low cost digital still camera. The radial lens distortion parameters are \(k_1=8.06244e-08\), \(o_x=512\) and \(o_y=384\).

Figure A.3 Camera 3 of the multi-view images “Livingroom”.

n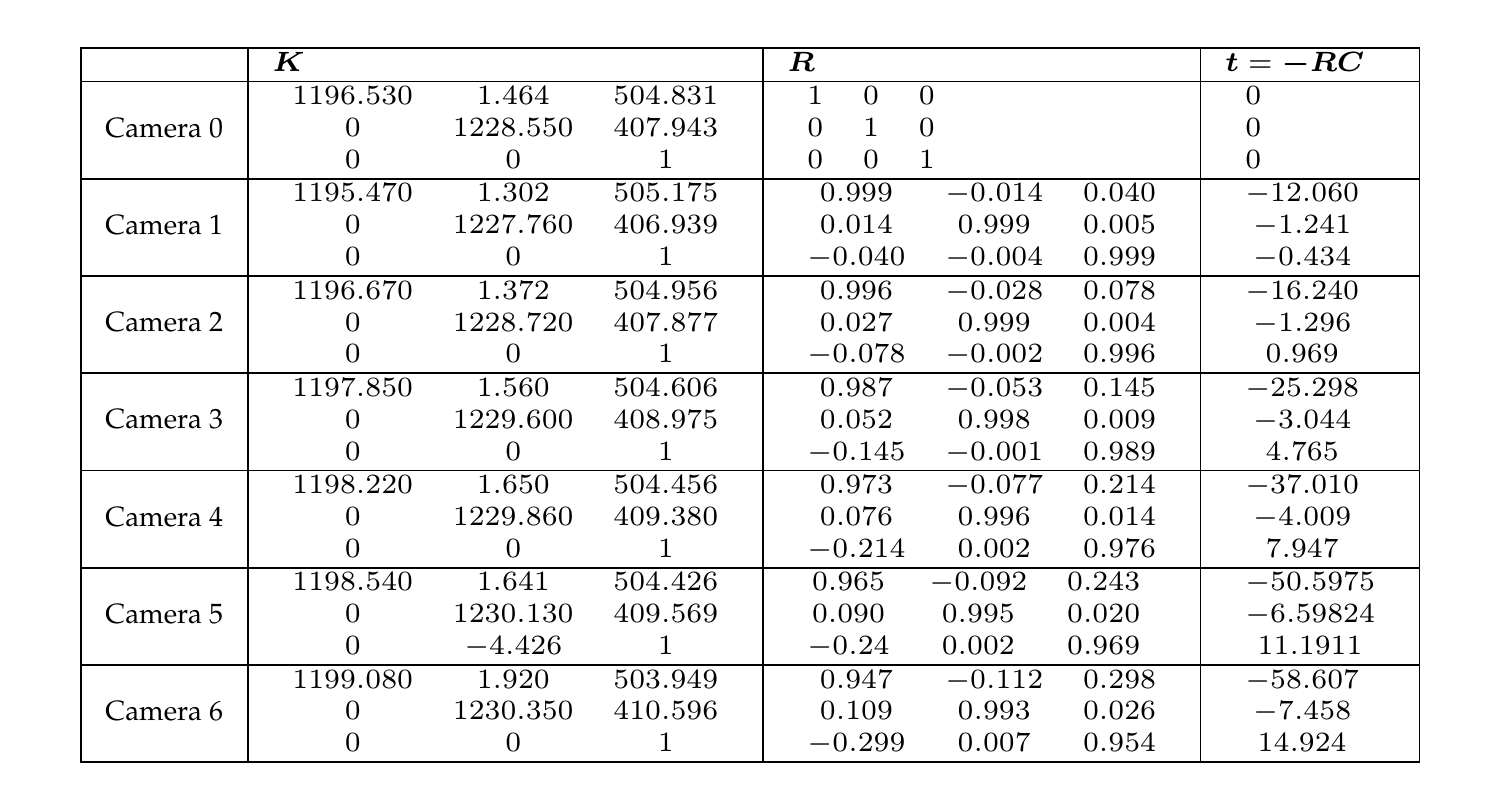

Table A.3 Calibration parameters of the multi-view images “Livingroom”.

“Cones” and “Teddy”

Figure A.4 illustrates the multi-view images “Cones” and “Teddy”, respectively. These multi-view images are available at the Stereo Vision research page [37] and are provided without calibration parameters. The resolution of the images is \(450 \times 375\) pixels.

(a) (b) Figure A.4 Leftmost view of the multi-view images (a) “Cones” and (b) “Teddy”.

References