H.264-Based Depth and Texture Multi-View Coding

[chapter:multiview_coding] This chapter concentrates on the compression of multi-view depth and multi-view texture video, based on predictive coding. To exploit the inter-view correlation, two view-prediction tools have been implemented and used in parallel: a block-based disparity-compensated prediction and a View Synthesis Prediction (VSP) scheme. Whereas VSP relies on an accurate depth image, the block-based disparity-compensated prediction scheme can be performed without any geometry information. Our encoder employs both strategies and adaptively selects the most appropriate prediction scheme, using a rate-distortion criterion for an optimal prediction-mode selection. The attractiveness of the encoding algorithm is that the compression is robust against inaccurately-estimated depth images and requires only two reference cameras for fast random-access to different views. We present experimental results for several texture and depth multi-view sequences, yielding a quality improvement of up to 0.6 dB for the texture and 3.2 dB for the depth, when compared to solely performing H.264/MPEG-4 AVC disparity-compensated prediction.

Introduction

Current 3D video systems can be coarsely divided into two classes. The first class focuses on the 3D-TV application and relies on the 1-depth/1-texture 3D video representation format. Specifically, by combining one texture video and one depth video, synthetic views can be rendered using an image rendering algorithm and, they can be visualized using a stereoscopic display. The compression and transmission of the 1-depth/1-texture approach was recently standardized by Part 3 of the MPEG-C video specifications [76]. As already mentioned in the introductory chapter, the 1-depth/1-texture relies on a single texture video combined with a corresponding depth video signal. However, considering a video scene with rich 3D video geometry, rendered virtual views typically show occluded regions that were not captured by the reference camera. We have seen in the previous chapter that occluded regions can be accurately rendered by combining multiple source images. Therefore, a second class of 3D video systems is based on multiple texture views of the video scene, called N-texture representation format [9]. The N-texture approach forms the basis for the Multi-view Video Coding (MVC) standard currently developed by the Joint Video Team (JVT) [10] within the ITU and ISO MPEG. However, the MVC standard does not involve the transmission of depth sequences, thereby reducing the quality of the rendered images. For this reason, a third class of 3D video systems is based on the N-depth/N-texture 3D video representation format. In October 2007, the Join Video Team (JVT) started an ad-hoc group, specifically focusing on the compression of N-depth/N-texture 3D video [77]. Our work in this chapter originates from the period 2006-2007.

Let us now discuss the problem of N-depth/N-texture multi-view video coding in more detail. A major problem when dealing with N-texture and N-depth video signals is the large amount of data to be encoded, decoded and rendered. For example, an independent transmission of 8 views of the “Breakdancers” sequence, using an H.264/MPEG-4 AVC encoder, requires about \(10~Mbit/s\) and \(1.7~Mbit/s\) with a PSNR of \(40~dB\) for the texture and depth data, respectively.¹² Given this resolution and the limited frame rate for the experimental sequences, it can be directly concluded that the bit rate is relatively high. Therefore, coding algorithms enabling an efficient compression of both multi-view depth and texture video are necessary. In a typical multi-view acquisition system, the acquired views are highly correlated. As a result, a coding gain can be obtained by exploiting the inter-view dependency between neighboring cameras.

In this chapter, we propose a multi-view coding algorithm that is based on two different approaches for the predictive coding of views. We employ two approaches for predictive coding for handling varying multi-view acquisition conditions (small or large baseline distance) and varying 3D depth image quality. The first predictive coding tool is based on a block-based disparity-compensated prediction scheme (the difference between motion and disparity compensation is further elaborated in the next section). The advantages of this predictive coding tool are that it does not require a geometric description of the scene and it yields high coding efficiency for multi-view sequences with small baseline distance. The second predictive coding tool is based on a View Synthesis Prediction algorithm (VSP), that synthesizes an image as captured by the predicted camera [78], [79]. The advantage of the VSP algorithm is that it enables the prediction of views for large baseline distance sequences. The proposed encoder employs both approaches and adaptively selects the most appropriate prediction scheme, using a rate-distortion criterion for an optimal prediction-mode selection. To evaluate the efficiency of the VSP predictive coding tool, we have integrated VSP into an H.264/MPEG-4 AVC encoder. We particularly emphasize that previous contributions on multi-view video coding have mainly focused on multi-view texture video. However, the problem of multi-view depth video coding has been hardly investigated and forms therefore an interesting topic.

This chapter is organized as follows. We commence with a short survey of previous multi-view texture coding approaches. In the same section, the performance of the surveyed multi-view coding algorithms is evaluated for both texture and depth compression. Afterwards, Section 5.3 and Section 5.3.3 describe the integration of two predictive coding algorithms, i.e., block-based disparity-compensated prediction and VSP, into an H.264/MPEG-4 AVC encoder. Experimental results are provided in Section 5.4 and the chapter concludes with Section 5.5.

Multi-view video coding tools

In this section, we provide an overview of the multi-view compression coding approaches, some of which have been investigated in the scope of the MVC standard [80] and we perform a comparison of their performance.

Disparity-compensated prediction

Generally, it is accepted that multi-view images are highly correlated so that a coding gain can be obtained [81]. To exploit the inter-view correlation, a typical approach is to perform a block-based disparity-compensated prediction. Similar to a block-based motion-compensated prediction, a block-based disparity-compensated prediction estimates (for each block) a displacement/disparity vector between a predicted view and a main reference view. The approach of using a disparity-compensated prediction was earlier adopted in the MPEG-2 multi-view profile [82]. The disparity-compensated prediction scheme assumes that the motion of objects across the views corresponds to a translational motion model. For a short baseline camera distance, this assumption on translational motion is usually valid. However, considering a wide baseline multi-view sequence, the motion of objects cannot always be accurately approximated by a simple translation. In such a case, the temporal correlation between two consecutive frames may be higher than the spatial correlation between two neighboring views. To evaluate the temporal and spatial inter-view correlation, a statistical analysis of the block-matching step has been carried out [81]. In the discussed analysis, the block-matching step refers to finding the block that is most similar to the selected reference block in the neighboring views or the time-preceding frames. In the case the prediction block is located in a time-preceding frame, the block is temporally predicted. Alternatively, if the predicted block is located in a neighboring view/frame, the block is spatially predicted. Experimental results of the statistical analysis in [81] show that the image blocks are temporally predicted in 63.7% and 87.2% of the cases, for the “Breakdancers” and “Ballet” sequences, respectively. As a result, depending on the multi-view sequences properties, in particular, the baseline-camera distance, it is more appropriate to exploit the temporal correlation rather than the spatial inter-view correlation. Therefore, we propose a prediction structure that adequately exploits both the temporal and spatial inter-view correlation should be employed.

Prediction structures

Let us now discuss several prediction structures that exploit both the temporal and spatial inter-view correlations. To adequately exploit both correlations, several multi-view coding structures have been explored within the MVC framework [83].

A. Simulcast coding

To perform multi-view coding, a first straightforward solution consists of independently encoding the multiple views, called simulcast coding. The prediction structure of a simulcast coding algorithm is illustrated by Figure 5.1(a), where each view is independently coded and compression only exploits temporal redundancy. One advantage of simulcast coding is that standard video encoders can be used for multi-view coding. However, simulcast coding does not exploit the correlation between the views. Because of its simplicity, simulcast coding is typically employed as a reference for comparisons of coding performance. For example, an evaluation procedure based on a simulcast compression of the views was initially proposed within the MVC framework as a coding performance anchor [32].

B. Hybrid motion- and disparity-compensated prediction structure

As a second approach, it has been proposed [11], [12], [84] to simultaneously exploit the temporal and inter-view correlations. To this end, a selected view is predicted from a time-preceding frame or from a neighboring view, using motion- or disparity-compensated prediction, respectively. Therefore, by employing multiple reference frames, temporal and inter-view correlations can be simultaneously exploited. The prediction structure of this hybrid motion- and disparity-compensated prediction structure is illustrated by Figure 5.1(b). In the following, we denote this Motion- and Disparity-Compensated prediction structure as an “MaDC prediction structure”. In practice, at least two reference frames should be employed and stored in the Decoded Picture Buffer (DPB) of an H.264/MPEG-4 AVC encoder. Therefore, it can be noted that the H.264/MPEG-4 AVC architecture features the advantage of enabling view-prediction from multiple reference frames. Additionally, by employing the H.264/MPEG-4 AVC rate-distortion optimization, the optimal (in a rate-distortion sense) reference frame can be selected for each image block. Similar multiple prediction structures have been recently reported to the MVC framework [83]. One of these prediction structures exploits also the spatial and temporal redundancy by performing a hierarchical bi-directional prediction of the views (hierarchical B-picture) [12]. This prediction structure was then integrated into the MVC reference software [85] and constitutes an essential coding tool of the MVC software. (a)

(b)

Figure 5.1 (a) Simulcast prediction structure and (b) MaDC prediction structure for multi-view coding.

C. Experimental comparison of prediction structures

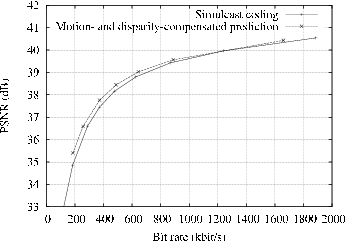
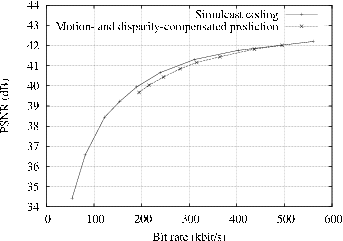
We now present experimental comparison of two texture and depth multi-view encoded sequences, using the previously introduced prediction structures. We start by discussing the rate-distortion curves of the texture multi-view sequences, as shown by Figure 5.2. For coding experiments, we have employed the open-source H.264/MPEG-4 AVC encoder x264 [86]. The arithmetic coding algorithm CABAC was enabled for all experiments and the motion search was \(32 \times 32\) pixels. The Group Of Pictures (GOP) size is set to 25 frames and the GOP structure is defined as IBBP. Finally, the number of reference frames is set to 2 and the first 25 frames of the sequences are used for compression. First, for the “Breakdancers” sequence, it can be observed that the MaDC prediction structure slightly outperforms the simulcast prediction structure. For example, an MaDC prediction structure yields a quality improvement of 0.2 dB at a bit rate of 700 kbit per view with respect to simulcast coding. However, considering the “Ballet” sequence, no coding gain is observed, instead a small loss occurs. Such a result simply emphasizes that the temporal correlation between consecutive frames is more significant than the inter-view correlation between neighboring views (as highlighted by the statistical analysis discussed in Section 5.2.1). Therefore, the overhead involved by the usage of multiple reference frames (e.g., reference frame index for each block) decreases the coding performance. For comparison, the MVC reference software yields a coding improvement of 0.25 dB and 0.05 dB for the “Breakdancers” and “Ballet” sequences, respectively [87]. Therefore, the presented MaDC prediction structure yields a coding efficiency similar to the MVC reference software. Additionally, although significant coding improvements can be obtained for multi-view sequences with short baseline camera distances [83], experimental results show that neither the MVC encoder nor the MaDC prediction structure yield significant coding improvements for wide baseline multi-view sequences. As confirmed by the coding experiments reported to the Joint Video Team [87], this conclusion is especially true for the wide baseline multi-view sequence “Ballet”.

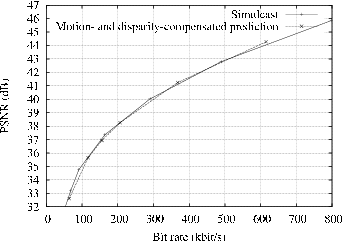
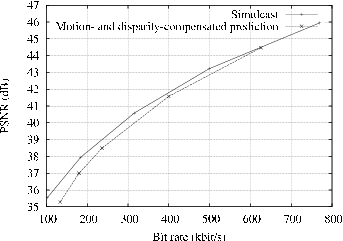
Let us now consider the compression of multi-view depth sequences. Considering the rate-distortion curves of the depth multi-view sequences “Breakdancers” and “Ballet”, it can be observed that an MaCD prediction structure does not yield a coding improvement over simulcast coding (see Figure 5.3). In the case of such wide baseline sequences, the depth image sequences show high temporal correlation. As a result, a large percentage of macroblocks can be encoded using a motion SKIP coding mode, where the inter-view correlation is not exploited at all. In this mode, the depth signals are so stable over time that the transmission of macroblocks can be skipped and the contents of depth macroblocks are copied from the previous frame. This is particularly true for depth video, since depth signals have a smooth nature. For comparison with the MVC reference software, a coding improvement of 0.3 dB was obtained by the MVC software for the “Breakdancers” depth sequence [87]. However, similar to the presented coding structure, the MVC encoder yields no coding improvement (and even a slight degradation) for the “Ballet” depth sequence.

(a)

(b)

Figure 5.2 RD-curves of the texture sequences (a) the “Breakdancers” and (b) “Ballet” encoded using the simulcast and MaDC prediction structures.

(a)

(b)

Figure 5.3 RD-curves of the depth sequences (a) “Breakdancers” and (b) “Ballet” encoded using the simulcast and MaDC prediction structures.

Performance bounds

In the previous section, the rate-distortion efficiency of motion- and disparity-compensated coding of multi-view video has been investigated. However, the theorical bound for the coding of multi-view video has not been addressed, so that the theorical gain in coding performance is not known. Considering the case of single-view video coding, a mathematical framework that establishes the coding performance bound of motion-compensated predictive coding was proposed [88]. This mathematical framework was later extended for evaluating the theoretical rate-distortion bounds for motion- and disparity-compensated coding of multi-view video [89]. In the discussed study, a matrix of pictures of M views and K temporally successive pictures is defined. Here, the parameter M indicates the Group of Views (GOV) size, for which the inter-view similarity between M neighboring views is exploited. For example, the case M=1 corresponds to a simulcast compression of the views. To evaluate the rate-distortion bounds, the impact of various temporal GOP and spatial GOV sizes is explored. Results of the analysis shows that the rate-distortion gain significantly depends on the properties of the multi-view sequence. Specifically, in the case the inter-view redundancy is exploited for 8 views (M=8), a theoretical coding gain ranging from 0.01 to 0.08 bit/pixel/camera can be obtained. Therefore, the coding gain can vary significantly, but for practical cases, such as a GOP=8 or even larger, the coding gain is rather limited. For the multi-view sequences investigated in this thesis, a limited theoretical coding gain of 0.01 and 0.02 bit/pixel/camera is obtained at 40 dB for the “Breakdancers” and “Ballet” sequences, respectively ¹³. Additionally, the analysis highlights that exploiting the interview redundancy across a varying number of views (M=4 or M=8) does not significantly alter the coding-performance bound. Instead, it was shown that the temporal redundancy constitutes a very important factor in the theoretical coding-performance bound for wide baseline camera distances.

Coding efficiency versus random access and decoding complexity

In the previous section, the compression efficiency of existing multi-view coding structures was investigated in a straightforward fashion. However, coding efficiency is not the only important aspect for consideration. A second important feature is the ability for users to randomly access views in the encoded bit stream. In practice, considering a free-viewpoint video system, this feature enables a user to switch viewpoints at interactive rates, i.e., at the frame rate of the video. A third aspect is the complexity of the multi-view video decoder, either implemented on a regular computer or as embedded system within a (low-cost) consumer electronics product. Therefore, the design of the free-viewpoint video system is driven by three aspects: (1) compression efficiency, (2) random-access, i.e., low-delay access to a desired view and (3) low complexity of the multi-view decoder. These three system aspects should be balanced at design time. Given the importance of these aspects, we discuss them in more detail in this section.

A. Decoding complexity versus low-delay access.

Because switching viewpoints should be performed at the frame rate of the video, the decoding of the desired views should be completed within a frame time (e.g., within 1/25 seconds). Therefore, to keep the delay of decompression reasonably low, the number of dependencies should be limited. Although the current monocular video coding standards do provide some random-access capabilities (insertion of intra-coded frames), these were designed for robustness reasons and fast channel switching and as such, are insufficient for the free-viewpoint video application. Specifically, depending on the processing capabilities of the decoder and the periodicity of inserted intra-coded frames ¹⁴, a simulcast compression of the views may not enable the user to switch viewpoints at the frame rate of the video. One approach to allow a user to switch viewpoints at the frame rate of the video is to prepare and decode all views prior to the user-selection of the view. However, this approach involves the parallel decompression of all views and all of its reference views. For a simulcast prediction structure, this approach implies the instantiation of one H.264/MPEG-4 AVC decoder for each view and thus a high computational complexity. Hence, the multi-view video player should be able to handle simultaneously multiple H.264/MPEG-4 AVC decoders, or be able to decode the user-selected view and all of its reference frames within the delay tolerated by the user. Alternatively, a prior decompression of the views encoded using an MaDC prediction structure, requires the decompression of the user-selected view/frame and all of its reference frames. Therefore, the complexity of such a free-viewpoint video decompression system grows as \(O(M)\) where \(M\) corresponds to the number of views and their reference views/frames. In the case the system cannot handle the parallel decompression of all views, the desired view is rendered with delays. Examples of coding scenarios will be provided in Section C in the sequel.

B. Compression efficiency versus random access.

Typically, random access is obtained by reducing the coding dependencies between encoded frames and it can be implemented by periodically inserting intra-coded frames. Therefore, there exists a trade-off between coding efficiency and random-access capabilities and an appropriate coding structure should be selected such that it balances both the coding efficiency and the random-access capabilities. To provide random access to an arbitrary view while still exploiting the temporal and inter-view correlations, we propose to use predefined main views as reference frames from which neighboring secondary views are predicted (see Figure 5.4). A closer inspection of the proposed coding structure reveals that temporal correlation is exploited only by two main views. Alternatively, the secondary views exploit only the spatial inter-view correlation. Consequently, by exploiting an appropriate mixture of temporal and inter-view predictions, views along the chain of cameras can be randomly accessed. However, it should be noted that this approach is obtained at the expense of a loss in coding efficiency. Thus, the number of reference main views should be appropriately selected, such that the compression efficiency is not dramatically reduced. The number of reference main views can range from \(1\) to \(N-1\), where the exact number depends on the tolerated rendering latency and depending on the expected compression efficiency (here, \(N\) corresponds to the number of views). Additionally, the illustrative example presented in this chapter shows that the number of reference main views also significantly depends on the properties of the sequences.

C. Scenarios for selecting prediction structures.

From the previous discussion, four scenarios for adequately selecting a prediction structure can be distinguished. The first scenario consists of encoding a short baseline multi-view sequence and tolerating a high delay for accessing the views. In this scenario, an MVC encoder or an MaDC prediction structure should be employed because they feature a high coding performance. The second scenario consists of encoding a short baseline multi-view sequence but requiring a low delay for accessing a desired view. This scenario implies that a limited rendering delay is tolerated by the viewer so that a complex prediction structure should not be employed. To obtain a low-delay access, the proposed coding structure from Figure 5.4. However, to correctly balance the low-delay access with the coding efficiency, a significant number of main views should be employed, e.g., \(N/3\), where \(N\) corresponds to the number of views. In the case the compression performance should be preserved, the number of main views can be as high as \(N\). The third scenario consists of encoding a wide baseline multi-view sequence and tolerating a high delay for rendering. In this case, a high delay tolerated by the viewer does not necessarily imply that using a complex prediction structure is beneficial. For example, the MVC encoder and the MaDC prediction structure could not improve the coding efficiency for the wide baseline distance sequence “Ballet”, when compared to a simulcast coding of the views (see Figure 5.2 and the JVT input document [87]). Thus, for simplicity, simulcast compression may be prefered in this scenario. The fourth scenario consists of encoding a wide-baseline multi-view sequence and not tolerating a high latency for accessing and rendering images. In this last case, the proposed prediction structure from Figure 5.4 should be employed because a limited number of coding dependencies is used. Furthermore, depending on the desired coding efficiency, the system designer can select the number of reference main views, such that the coding efficiency and low-delay access is appropriately balanced. In this chapter, we provide an illustrative example, where two reference main views are used. However, even this simple case will clearly illustrate the trade-off between sequence properties and compression efficiency, as our experimental results will show later in this chapter.

Figure 5.4 Coding structure that allows motion- and disparity-compensated prediction with random access to an arbitrary view. Main views exploit the temporal correlation while the secondary views exploit the inter-view correlation.

View Synthesis Prediction (VSP) for N-depth/N-texture coding

In this section, we propose a novel multi-view encoder, based on H.264/MPEG-4 AVC, that employs two different view-prediction algorithms in parallel. In this section, the text and algorithm development concentrates on texture coding for simplicity reasons and because the author developed the algorithm in this way. However, after the design and experiments, it appeared that virtually all descriptions equally apply to the compression of multi-view depth sequences. The reader should therefore interpret the text as being applicable to both depth and texture. At the end of this section, a contribution which is specific to depth signals is appended.

Predictive coding of views

The first inter-view prediction technique is the disparity-compensated prediction scheme. A major advantage of the disparity-compensated prediction is that a coding gain is obtained when the baseline distance between cameras is small. Additionally, the disparity-compensated predictor does not rely on the geometry of multiple views, so that camera calibration parameters are not required. However, we have shown in Section 5.2.2 that the disparity-compensated prediction scheme does not always yield a coding gain, especially for wide baseline distance camera setting. A reason for this is that the translational motion model, employed by the block-based motion-compensated scheme, is not sufficiently accurate to predict the motion of objects with different depths.

The second alternative, i.e., a View Synthesis Prediction (VSP) scheme, is based on a view-synthesis algorithm that renders an image as seen by the predicted camera [78], [79]. The advantage of the view-synthesis prediction is that the views can be better predicted, even when the baseline distance between the reference and predicted cameras is large, thereby yielding a high compression ratio. However, as opposed to the previous approach, the multi-camera acquisition system needs to be fully calibrated prior to the capturing session and relies on an reasonably accurate depth image. Additionally, because depth estimation is a complicated task, the depth images may be inaccurately estimated, thereby reducing the view-prediction quality. Since VSP is new in the discussion, we further concentrate on its integration into a multi-view video encoder based on H.264/MPEG-4 AVC.

Incorporating VSP into H.264/MPEG-4 AVC

Important requirements of the view-prediction algorithm are that (a) it should be robust against depth images which are inaccurately estimated, and (b) a high compression ratio should be obtained for various baseline distances between cameras. As discussed above, both presented view-prediction algorithms have their limitations and cannot be used under variable capturing conditions. Therefore, our novel strategy is to use both algorithms selectively on an image-block basis, depending on their current coding performance.

An attractive approach to support coding efficiency is to integrate both prediction techniques, i.e., the View Synthesis Prediction (VSP) and Disparity Compensated Prediction (DCP), and then select the best prediction for each block. It should be noted that both prediction techniques employ two different reference frames: DCP uses the main view, whereas VSP applies the synthesized image. Thus, each block of a frame can be predicted by one of the reference frames stored into the reference frames buffer (also known as Decoded Picture Buffer (DPB)). A disadvantage of such a multi-view encoder is that VSP generates a prediction image that does not necessarily minimize the prediction residual error, so that the complete scheme would not yield the minimum residual error accordingly. Consequently, the adopted system concept is modified as follows.

• First, the VSP provides an approximation of the predicted view using a pre-selected image rendering technique.

• Second, the DCP refines the view-synthesis prediction using a block-based disparity-compensated prediction.

At the refinement stage, the search for matching blocks is performed in a region of limited size, e.g., \(32 \times 32\) pixels. In contrast to this, the disparity between two views in the “Ballet” sequence can be as high as 50 pixels. Figure 5.5 portrays an overview of the resulting proposed coding architecture.

Figure 5.5 Architecture of an H.264/MPEG-4 AVC encoder that adaptively employs a block-based disparity-compensated prediction or view-synthesis prediction followed by a prediction refinement. The main view and the synthesized view are denoted Ref and W(Ref), respectively.

There are multiple advantages for using an H.264/MPEG-4 AVC encoder. First, because the H.264/MPEG-4 AVC standard enables that each macroblock can be encoded using different coding modes, occluded regions in the predicted view can be efficiently compressed. More specifically, occluded pixels cannot always be predicted with sufficient accuracy. In this case, the algorithm encodes an occluded macroblock in intra-mode. Alternatively, when the prediction accuracy of occluded pixels is sufficient, the macroblock is encoded in inter-mode. Summarizing, the flexibility of H.264/MPEG-4 AVC provides a suitable framework for handling the compression of occlusions. Second, in the case that the depth image is not estimated accurately, the VSP coding mode is inefficient and will be simply not selected. Hence, the criterion automatically leads to the correct coding mode selection. Third, the prediction mode of each image block is implicitly specified by using the reference frame index, so that no additional information has to be transmitted. Specifically, as previously highlighted, the VSP and the DCP coding algorithms employ two different reference frames: the synthesized image and the main reference view, respectively. Because these reference frames are stored into the DPB, an image block can be predicted using, either the first (DCP), or the second (VSP) frame buffer. The selection of the prediction scheme is therefore indicated to the decoder by the index of the reference frame, which is an integral part of the H.264/MPEG-4 AVC standard. Fourth and additionally, the selection of the prediction tool is performed for each image block using a rate-distortion criterion. In practice, the rate-distortion criterion can be based on an R-D optimized coding-mode selection, as implemented in a standard H.264/MPEG-4 AVC encoder. Thus, the H.264/MPEG-4 AVC standard offers sufficient flexibility in providing the appropriate coding modes for optimal matching with the varying prediction accuracies of VSP and DCP.

Multi-view depth coding aspects when using VSP

A multi-view depth image sequence has correlation properties similar to a multi-view texture sequence. More specifically, because each depth image represents the depth of the same video scene, all depth images are correlated across the views. This property is similar to the discussion on multi-view texture coding in the previous section. This motivates why the same coding concept for exploiting inter-view correlation can be equally applied to both texture and depth coding. As a consequence of the above, a coding gain for depth signals can be obtained by exploiting depth inter-view correlation. Similar to multi-view texture coding, the multi-view depth coding algorithm employs the two different view-prediction algorithms, i.e., the DCP and VSP schemes. The most efficient prediction method is then selected for each image block using a rate-distortion criterion. As opposed to recent contributions in literature, the presented solution is the first to employ a view-synthesis prediction scheme for encoding multi-view depth sequences.

A further benefit of this approach is that depth signals are relatively smooth and thus can be accurately predicted using a view-synthesis algorithm. In this aspect, the predictive coding of depth signals is typically more efficient than for multi-view texture signal, since view-synthesis prediction of texture signals may not always be able to accurately predict fine texture. A last advantage is that the predictive coding of depth views does not require the transmission of side information, but instead performs the prediction of neighboring depth views using the depth main view only. Figure 5.6 shows an overview of the described depth-coding architecture. This figure is nearly the same as the coding block diagram for texture. There is only one major difference: to perform view-synthesis prediction, the depth compression requires only camera parameters as input, whereas the texture compression needs both camera parameters and a reference depth image. In the depth coding loop, the reference main view enables the simultaneous prediction of multiple secondary views without any side informations such as motion vectors. Let us now evaluate the results of DCP- and VSP-based coding algorithms for depth and texture multi-view signals.

Figure 5.6 Architecture of the extended H.264/MPEG-4 AVC encoder that adaptively employs the previously encoded depth image \(D_{t-1}\) or the corresponding warped image \(W(D_{t-1})\) as reference frames.

Experimental results

Conditions

For evaluating the performances of the proposed multi-view texture- and depth-coding algorithms, experiments were carried out using the “Ballet” and “Breakdancers” texture and depth multi-view sequences. The presented experiments investigate the impact of the prediction accuracy on the rate-distortion performance. For each presented rate-distortion curve, the compression of multi-view images is performed under three different conditions indicated as follows.

1. “Simulcast”: the compression of multi-view depth and texture video is performed using a simulcast coding structure ,¹⁵ i.e., limited random-access capabilities. (Figure 5.1(a))

2. “DCP”: the prediction of depth and texture views is carried out using only the H.264/MPEG-4 AVC block-based disparity-compensated prediction. To enable better random-access capabilities, the coding structure illustrated by Figure 5.4 is employed.

3. “DCP/VSP”: the prediction scheme (VSP or DCP) is carried out adaptively, using a rate-distortion criterion for an optimal prediction-mode selection. To enable better random-access capabilities, the coding structure illustrated by Figure 5.4 is employed.

For the coding experiments, we have employed the open-source H.264/MPEG-4 AVC encoder x264 [86] using main profile encoding. The arithmetic coding algorithm CABAC was enabled for all experiments and the motion search area was \(32 \times 32\) pixels. We have set the number of reference frames to 2: one reference for the block-based disparity prediction and a second for the view-synthesis prediction. The Group Of Pictures (GOP) size is set to 25 frames and the GOP structure is defined as IBBP (as proposed in the JVT document [32]). Thus, as opposed to the JVT input document [87] that investigates the compression performance of MVC for multi-view video plus depth, no hierarchical B-pictures are employed in the presented experiments. Prior to rendering, the reference depth is encoded with quantizer setting \(QP=29\). An algorithm for optimally selecting this quantizer setting is proposed in Chapter 7. It should be noted that depth images should be encoded at a relatively high quality to avoid ringing-artifacts along object borders in the depth map. This prevents that rendering artifacts occur in the synthesized view. This remark is similar to the conclusions related to recent depth compression results [70], [91]. Because depth data is necessary for 3D rendering in any case, it can be assumed that depth images are transmitted even in the case that no view-synthesis prediction is employed. Hence, employing the view-synthesis prediction does not involve any bit-rate overhead. Therefore, it should be noted that the presented rate-distortion curves for texture sequences do not include the bit rate of depth images.

Experimental results for multi-view texture coding

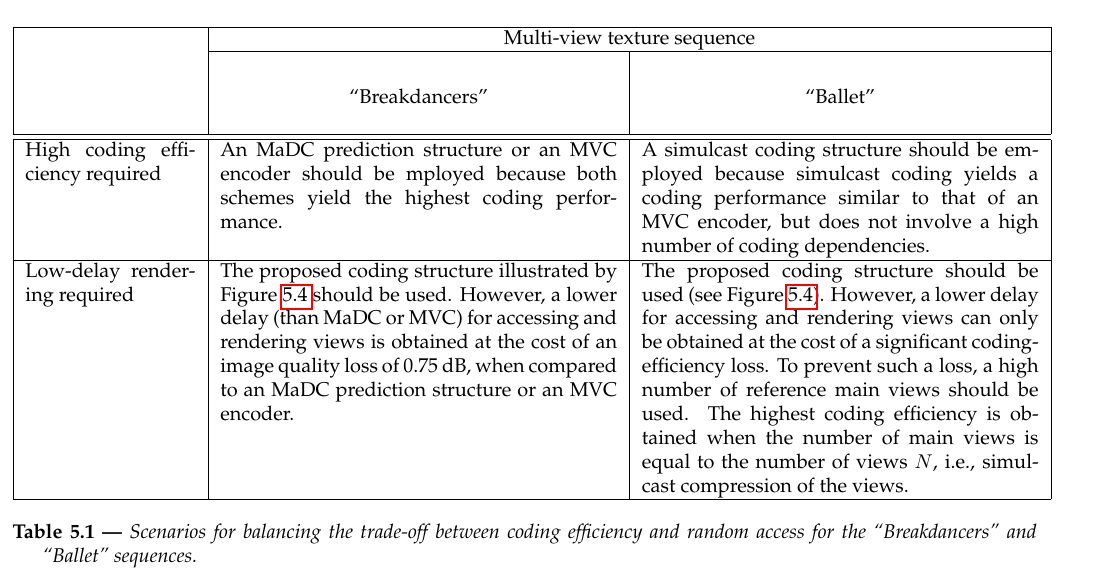
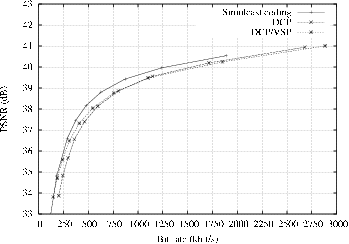
The result of the comparison for multi-view texture compression is provided by Figure 5.7.

Comparison of “DCP” with respect to “DCP/VSP”.

First, it can be observed that the proposed “DCP/VSP” algorithm consistently outperforms the “DCP” scheme. For example, observing the “Breakdancers” and “Ballet” rate-distortion curves (Figure 5.7(a) Figure 5.7(b), it can be seen that the “DCP/VSP” algorithm yields a quality improvement of 0.6 dB and 0.2 dB at a bit rate of 250 kbit/s and 500 kbit/s, respectively. However, at high bit rate of about 1 Mbit/s, no coding improvement is obtained. In that case, the view synthesis does not provide a sufficiently accurate prediction, so that the disparity-compensated prediction mode is mostly selected. The proposed VSP-based predictor is therefore mostly efficient at low bit rates and yields limited coding improvements at high bit rates, because it cannot accurately predict very fine textures. Summarizing, the adaptive “DCP/VSP” scheme always gives the best compression, but its gain is especially visible for low bit rates.

Comparison of “DCP/VSP” with respect to simulcast coding.

We especially evaluate the coding performance differences, while considering the random-access capabilities of the decoder. First, observing the rate-distortion curve of the “Breakdancers” sequence, it can be noted that the “DCP/VSP” coder yields slightly lower coding performances than the simulcast coding (0.2 dB at 250 kbit/s). In this case, the random-access capabilities are obtained at the cost of a limited coding-performance loss. For the “Ballet” sequence, it can be observed that random access capabilities can be obtained at the cost of a significant coding-performance loss. Such an important coding-performance loss can be explained by examining the properties of the “Ballet” multi-view sequence. More specifically, the “Ballet” sequence was captured using a wide baseline camera setup and depicts large foreground objects (the dancers). As a result, the sequence shows large occluded regions. Hence, the temporal correlation between consecutive frames is more important than the spatial inter-view correlation. This experimental result confirms the statistical analysis of [81], as discussed in Section 5.2.1. As suggested in Section 5.2.4, a solution to increase the coding efficiency is to employ more reference main views. In the extreme case, \(N\) reference main views may be employed to obtain the highest coding gain, where \(N\) corresponds to the number of views. For the “Ballet” sequence, this extreme case corresponds to a simulcast compression of the views and yields coding performances similar to those of an MVC encoder [87]. As a result, the system designer may employ the proposed coding structure, where the number of reference main views corresponds to a trade-off parameter that balances both the bit rate and the delay for accessing a desired view. This trade-off between coding efficiency and random access was discussed in Section 5.2.4. For each sequence, we summarize in Table 5.1 the corresponding scenarios discussed in Section 5.2.4 for selecting a prediction structure, such that the random access and coding efficiency are appropriately balanced.

(a)

(b)

Figure 5.7 RD-curves of sequences (a) “Breakdancers” and (b) “Ballet” encoded using simulcast, “DCP” and “DCP/VSP” coders.

Experimental results for multi-view depth coding

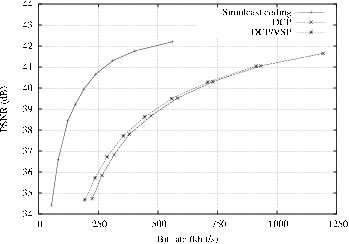
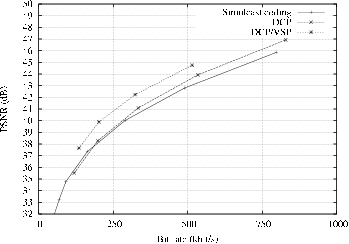
Figure 5.8 depicts the comparison results for the compression of multi-view depth sequences.

Comparison of “DCP” with respect to “DCP/VSP”.

First, it can be observed that the proposed “DCP/VSP” algorithm consistently outperforms the “DCP” scheme. For example, observing the rate-distortion curve of the “Breakdancers” depth image sequence (Figure 5.8(a)), the “DCP/VSP” algorithm yields a quality improvement of 1.6 dB and 1.2 dB at a bit rate of 250 kbit/s and 500 kbit/s, respectively. For the “Ballet” depth image sequence (Figure 5.8(b)), the proposed algorithm provides an image-quality improvement of 2.7 dB and 3.2 dB at a bit rate of 250 kbit/s and 500 kbit/s, respectively. Therefore, the view-synthesis predictive-coding algorithm brings significant coding improvements over a disparity-compensated prediction scheme. Such coding improvements can be explained by two factors. First, the view-synthesis algorithm correctly models the motion objects in the video scene. As a result, a view-synthesis prediction provides a more accurate prediction than a disparity-compensated prediction. Second, it should be reminded that consistency between depth images across the views was enforced during depth estimation (see Chapter 3). It can now be seen, that, besides depth-estimation accuracy, the inter-view consistency constraint for depth estimation also results in a coding efficiency improvement.

Comparison of “DCP/VSP” with respect to simulcast coding.

For the “Breakdancers” depth image sequence, it is interesting to note that the proposed “DCP/VSP” now outperforms simulcast depth coding. The obtained improvement is 1.6 dB and 1.7 dB at 250 kbit/s and 500 kbit/s, respectively. Summarizing, for the “Breakdancers” sequence, the proposed “DCP/VSP” algorithm provides random-access capabilities while improving the coding efficiency. For the “Ballet” sequence, a marginal coding loss of only 0.2 dB is obtained at 250 kbit/s and 500 kbit/s, respectively. Although no coding improvement can be reported for this particular case, the proposed algorithm still enables random access to different views as a remaining benefit.

(a)

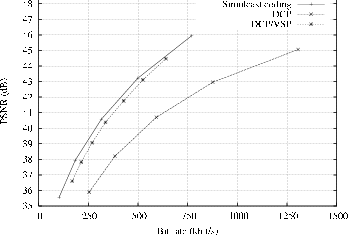
(b)

Figure 5.7 RD-curves of depth multi-view sequences for (a) “Breakdancers” and (b) “Ballet”, encoded using simulcast, “DCP” and “DCP/VSP” coders.

Conclusions

In this chapter, we have presented two predictive coding tools: the disparity-compensated prediction and the view-synthesis prediction. To increase the coding efficiency, the presented coding tools aim at exploiting the inter-view correlation by using various prediction structures. To this end, we have investigated the MaDC prediction structure that leads to a complex prediction structure and involves a large number of dependencies between the frames (see Figure 5.1(b)). We have therefore proposed an alternative coding structure that reduces the number of dependencies between the frames as shown by Figure 5.4. Related to this, we have discussed multiple scenarios for selecting an appropriate coding structure, fulfilling the requirements of (1) either high coding efficiency, or (2) low-delay access to a user-selected view.

Using the proposed prediction structure, we have presented a new algorithm for the predictive coding of multiple depth and texture camera views that employs two different view-prediction algorithms: a disparity-compen-sated prediction and a view-synthesis prediction. The advantages of the algorithm are that (1) the compression is robust against inaccurately estimated depth images and (2) the chosen prediction structure allows random access to different views. For each image block, the selection between the two prediction algorithms is carried out using a rate-distortion criterion. Furthermore, we have integrated the view-synthesis prediction scheme into an H.264/MPEG-4 AVC encoder, leading to an adaptive prediction, using either disparity-compensated prediction, or view-synthesis prediction. It was discussed that this integration can be performed smoothly and leads elegant advantages. The most relevant benefits are that the predictor selection is performed using the H.264/MPEG-4 AVC framework and that the coding mode selection is indicated by the reference frame index.

Experimental results have shown that the view-synthesis predictor can improve the resulting texture-image quality by up to 0.6 dB for the “Breakdancers” sequence at low bit rates, when compared to solely performing H.264/MPEG-4 AVC disparity-compensated prediction. However, we have found that the proposed coding structure yields a notable coding efficiency degradation for the “Ballet” texture sequence.

A major result of this chapter is that the view-synthesis prediction and its integration to the multi-view coding framework can be equally applied to the compression of multi-view depth images, thereby leading to a unified approach. The major difference between the texture and depth coding algorithm is that the depth prediction does not require any side information. As a bonus, the depth signals can be more easily predicted by the view-synthesis prediction because of their smooth properties and inter-view consistency. Experimental results have revealed that the proposed “DCP/VSP” coder yields a depth image quality improvement of up to a significant 3.2 dB when compared to the “DCP” coder. Finally, considering the multi-view depth sequence, we have indicated that random-access capabilities can be obtained without significant loss of coding efficiency or even coding gains.

At this point, it is relevant to briefly compare the results of this chapter with the recent developments of the MVC framework. The discussed MaDC prediction structure has a comparable performance to the MVC framework. For both MaDC and MVC encoders, a limited coding performance improvement occurs (when compared to simulcast compression) for wide baseline camera setups. For example, for the “Breakdancers” and “Ballet” multi-view sequences, an MVC encoder yields a compression improvement which ranges from 0.05 dB to 0.25 dB at 500 kbit/s for the texture compression, and -0.1 to 0.5 dB at 200 kbit/s for the depth compression. Bearing in mind that the MVC encoder has not provided a coding efficiency improvement for this wide baseline camera sequences, we have proposed to employ an appropriate number of reference main views that balances both the coding efficiency and the random-access capabilities.

The presented view-synthesis prediction scheme exploits both the depth and texture inter-view redundancy. The main arguments for employing this scheme are that it facilitates random access to a user-selected view (depth and texture) and we realize a significant improvement in multi-view depth compression. In Chapter 6, it will be shown that the the encoding of depth data is of crucial importance for rendering high-quality images. Subsequently, it will be described in Chapter 7 that the bit rate of the depth data constitutes an significant part of the total bit rate, so that improving the compression of depth signals will also improve the compression of the total data set.

References