Introduction

This chapter starts with an introduction to the fundamentals of three-dimensional (3D) imaging through an historical perspective. Following this, the chapter surveys 3D television and free-viewpoint video applications, after which we discuss 3D video systems recently proposed for those applications. Subsequently, we propose an alternative 3D video system and introduce its main components, i.e., the acquisition, the compression and the rendering. We conclude with an overview of the individual chapters, indicating the relevant publications and contributions.

Fundamentals of stereo visualization

The word “stereo” is derived from the Greek term “stereos” which can be translated by “solid” or “hard”. In the french language, this term gradually evolved to “stère de bois” which corresponds to a volumetric unit for a pile of wood. Stereo visualization thus refers to the visual perception of the solid three-dimensional (3D) properties of some objects. Developments in stereo visualization were initiated in 1838 when Sir Charles Wheatstone described the “Phenomena of Binocular Vision” [1]. Binocular vision relates to the interpretation of two slightly different views of the same object seen by both human eyes. From two different views, Wheatstone showed that the viewer can mentally reconstruct the object in three dimensions. To illustrate the concept, Wheatstone prototyped a device known as the “stereoscope”, which paints two different images of the same object directly onto the viewer retina. The initial implementation of the stereoscope, illustrated by Figure [1.1] is composed of two mirrors, A and A’, that project onto both eyes, the image of two different hand-drawn views E and E’ of a wire-frame cube. It is interesting to note that these early developments in stereoscopic visualization were made prior to the invention of photography.

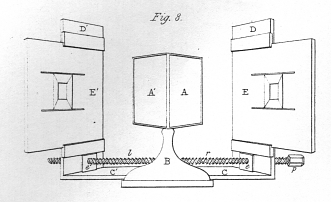
Figure 1.1 The initial implementation of the stereoscope is based on two mirrors that project two views of the same object onto both human eyes. From these two views, the human visual system mentally derives a three-dimensional representation of the cube.

The presented conceptual principle that relates two 2D images to a 3D representation of an object, can be extended. More specifically, it can be intuitively deduced that a more accurate 3D description of the object can be obtained from a set a multiple views. Therefore, stereoscopic 3D properties of a scene can be derived from multiple views or multi-view images captured by a set of multiple cameras. For example, the background and foreground orientation and the relative positions of objects in the 3D scene can be extracted by analyzing the multi-view images. Starting with this elementary concept, we can now outline several applications for multi-view images.

Applications of multi-view imaging

First, we introduce stereoscopic displays as a technology enabling several specific applications. Second, some applications to a free-viewpoint video system are provided, and finally, we illustrate the usefulness of multi-view images for video editing.

Stereoscopic displays

Stereoscopic displays allow the viewer to perceive the depth of the scene. This is achieved by displaying a left and right image/view in such a way that they are individually seen by the left and right eye. To obtain this result, several display technologies [2], including polarized displays, barrier-stereo displays and lenticular displays have been developed. Stereoscopic lenticular displays or multi-view lenticular displays, are based on a lenticular sheet which is precisely positioned onto an LCD display (see Figure 1.2(a). A lenticular sheet consists of an array of micro-lenses that directs the light of the underlying pixels in specific directions. Consequently, the viewing space in front of the display is divided into separate viewing zones, each of them showing a different image or view. The left and right eyes observe therefore a different view of the scene, thereby enabling the perception of depth. Figure 1.2(b) shows a three-view lenticular display that projects the light of three different pixels into three different viewing zones (two zones are drawn in the figure). To enable the viewer to watch the video scene from various viewpoints, nine-view lenticular displays have been introduced [3]. It can be readily understood that increasing the number of views involves a loss of image resolution so that there exists a trade-off between the number of views supported by the display and the resolution of the image. Recently, the development of high-definition (quad HD) LCD displays stimulated the usage of lenticular displays for various applications that we will be discussed in the sequel. On the short term, two-view displays for stereo-vision have gained strong popularity for 3D games and an early introduction to the 3D-TV market.

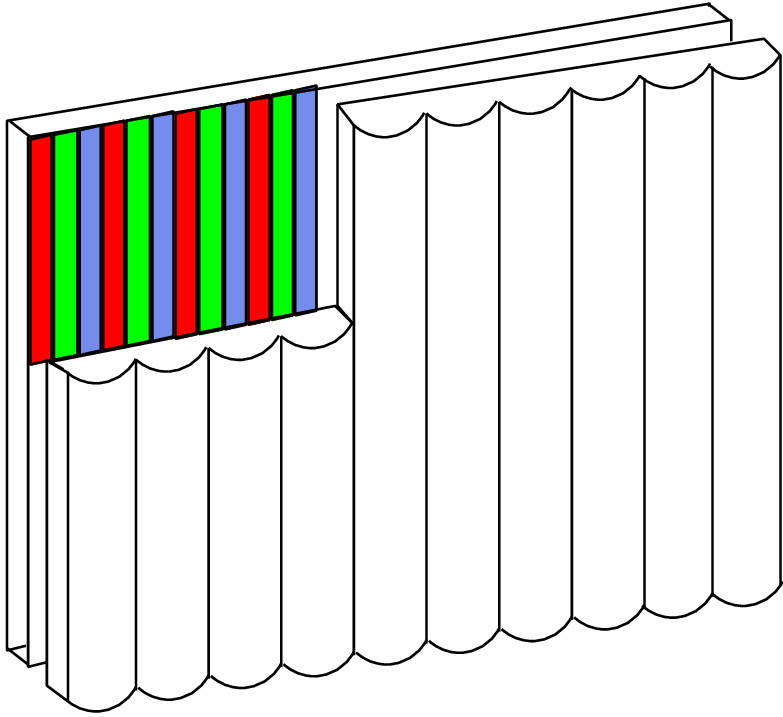
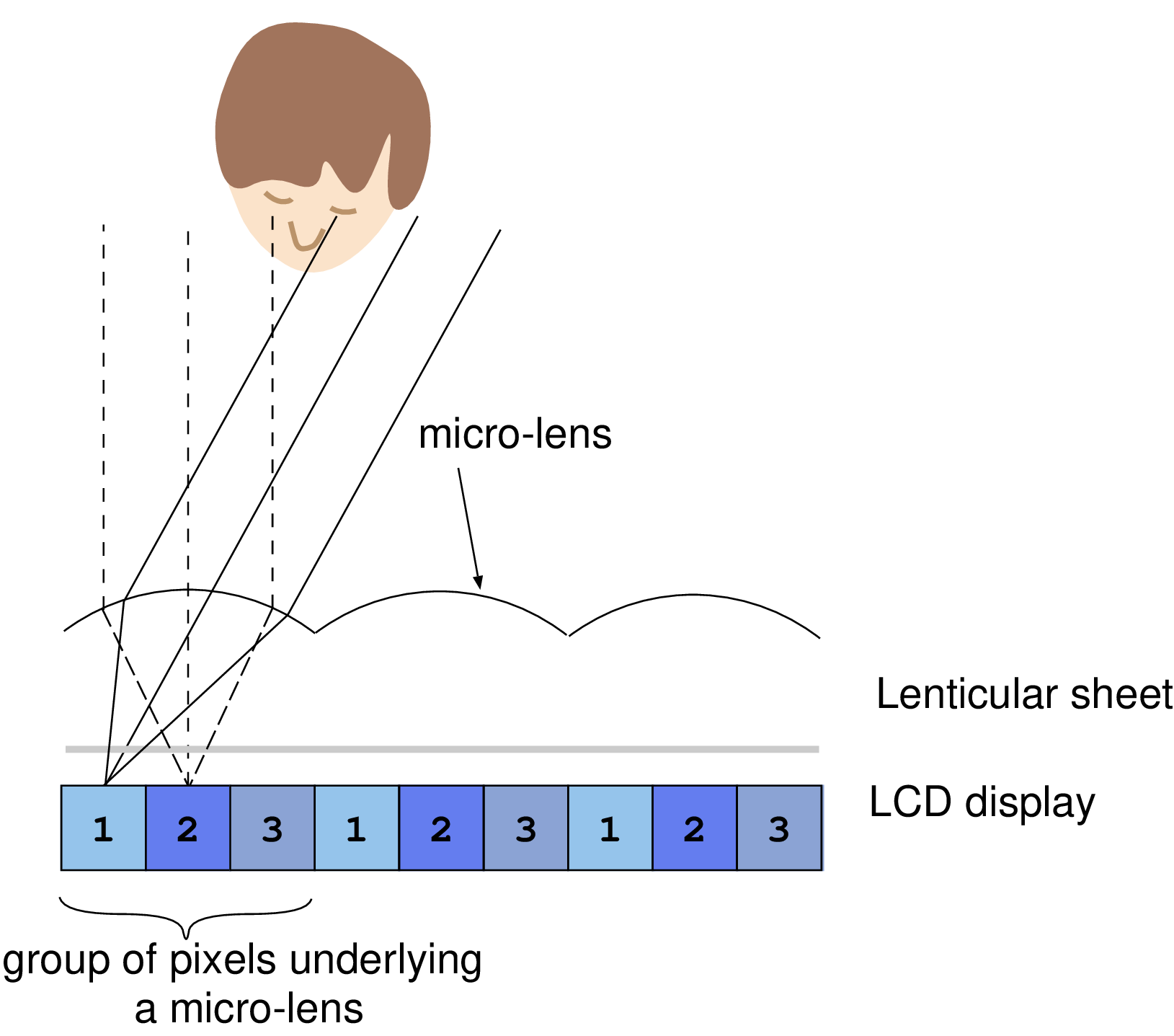
Figure 1.2(a) A lenticular display is composed of a lenticular sheet precisely positioned onto an LCD display. Figure 1.2(b) Multi-view lenticular display with three pixels/views covered by a micro-lens. Each view is projected into specific directions by the micro-lenses, so that the left and right eye see two different views.

The previously discussed stereoscopic displays enable several 3D applications, which are briefly outlined below.
3D-TV for home entertainment. Three-dimensional television (3D-TV) is expected to become a key application of stereoscopic displays by providing the viewer a feeling of immersion in the movie.
Video games. Similarly, stereoscopic displays greatly enhance the realism of video games by showing a 3D representation of the virtual scene and characters. One significant feature of video games is that a 3D description of the scene is provided by the game. Therefore, the usage of stereoscopic displays is readily supported by 3D video games featuring 3D geometric information.
Training and serious gaming systems. Another application for stereoscopic displays is the training of junior professionals. For example, it has been recently highlighted [4], that the usage of stereoscopic displays simplified the teaching of microscopical surgery to junior medical doctors. More specifically, microscopical surgery involves the manipulation of small structures of organs so that microscopes are usually employed. However, microscopes do not allow junior surgeons to perceive the depth as seen by the senior operating surgeon. Additionally, because junior surgeons lack the experience of anatomic proportions, no alternative cue can be employed to perceive the organ sizes and correctly locate the surgical plane. This example should obviously not be seen as the only application for training junior professionals. Instead, the example simply emphasizes that stereoscopic displays can be employed as a generic medium for training junior professionals such as medical doctors, pilots [5] or tele-operators [6]. This area can be extended to the emerging market of serious gaming that is between professional training and consumer gaming systems.

Free-viewpoint video

The free-viewpoint video application provides the ability for users to interactively select a viewpoint of the video scene. This can be performed by capturing the video scene from multiple viewpoints. However, a free-viewpoint video system does not impose that the selected viewpoint corresponds to an existing camera viewpoint. Therefore, a free-viewpoint video application breaks the restriction of showing an event only from the viewpoint of the cameras, but instead, allows a free navigation within the 3D video scene. For example, interesting applications include the selection of an arbitrary viewpoint for visualizing and analyzing sports or dynamic art (e.g., dance) actions.

Sports.

The ability to generate an arbitrary viewpoint is of particular interest for sports applications. For example, considering the case of a football match, it is often necessary for the referee to know the position of the players to ensure fair play. By rendering an appropriate viewpoint of the playing field [7], the player positions can be derived and illustrated using the virtual view.

Training video.

Free-viewpoint video technologies also simplify video training activities. For example, the training of dynamic activities such as martial arts or dancing can be simplified by allowing the trainee to select a viewpoint of the scene [8].

Video editing and special effects

Whereas in the previous subsection, the viewpoint was interactively chosen, in this subsection we summarize an application in which professional video editors manipulate time and place in one movie. For example, the multi-view image technology simplifies the production of special effects such as the “bullet time” effect. This effect provides the illusion to the viewer of freezing the time and gradually modifying the viewpoint of the scene. Such a special effect has been demonstrated in movies like “The Matrix”. Additionally, by exploiting the 3D information, it is possible to discriminate some background or foreground objects, which is known as z-keying. Using 3D information, video objects can be easily removed and re-inserted into the video elsewhere. Such video editing capabilities were demonstrated for a dancing video sequence [8]. Finally, it is also possible to insert synthetic 3D objects in the scene to obtain an augmented-reality video scene. This allows a free composition of a virtual scene as desired by the director while preserving the photo-realism of the movie.

Three-dimensional video systems layout

Because the previously discussed applications rely on multiple views of the scene, the 3D video technologies enabling these various applications do not exclude each other and can be integrated into a single 3D video system. Specifically, to enable 3D-TV or free-viewpoint video applications, several 3D video systems have been introduced. They can be classified into three classes with respect to the amount of employed 3D geometry.

A first class of 3D video systems is based on multiple texture views of the video scene, called N-texture representation format [9]. The N-texture approach forms the basis for the emerging Multi-view Video Coding (MVC) standard currently developed by the Joint Video Team (JVT) [10]. Due to the significant amount of data to be stored, the main challenge of the MVC standard is to define efficient coding and decoding tools ¹. To this end, a number of H.264/MPEG-4 AVC coding tools have been proposed and evaluated within the MVC framework. A first coding tool exploits the similarity between the views by multiplexing the captured views and encoding the resulting video stream by a modified H.264/MPEG-4 AVC encoder [11], [12]. A second coding tool equalizes the inter-view illumination to compensate for mismatches across the views captured by different cameras [13]. The latest description of the standard can be found in the Joint Draft 8.0 on Multi-view Video Coding [10]. One advantage of the above-mentioned N-texture representation format is that no 3D geometric description of the scene is required. Therefore, because 3D geometry is not used, this 3D video format allows a simple video processing chain at the encoder. However, such a 3D video representation format involves a high-complexity decoder for the following reason. A multi-view display supports a varying number of views at the input, which makes it impractical to prepare these views prior to transmission. Instead, intermediate views should be interpolated from the transmitted reference views at the decoder, where the display characteristics are known. To obtain high-quality interpolated views, a 3D geometric description of the scene is necessary, thereby involving computationally expensive calculations at the receiver side.

A second class of 3D video systems relies on a partial 3D geometric description of the scene [14]. The scene geometry is typically described by a depth map, or depth image, that specifies the distance between a point in the 3D world and the camera. Typically, a depth image is estimated from two images by identifying corresponding pixels in the multiple views, i.e., point-correspondences, that represent the same 3D scene point. Using depth images, new views can be subsequently rendered or synthesized using a Depth Image Based Rendering (DIBR) algorithm. Here, the term DIBR corresponds to a class of rendering algorithms that use depth and texture images simultaneously to synthesize virtual images. Considering a 3D-TV application, it is assumed that the scene is observed from a narrow field of view (short baseline distance between cameras). As a result, a combination of only one texture and one depth video sequence is sufficient to provide appropriate rendering quality (1-depth/1-texture). The 1-depth/1-texture approach was recently standardized by Part 3 of the MPEG-C video specification [15]. This system is illustrated in Figure 1.3. However, considering a video scene with rich 3D geometry, rendered virtual views typically show occluded regions that were not covered by the reference camera.

Figure 1.3 Overview of a 3D-TV video system that encodes and transmits one texture video along with one depth video (1-depth/1-texture). Note that the depth signal can be estimated using multiple texture camera views, of which only one view is transmitted.

A third class of 3D video systems addresses the occlusion problem by combining the two aforementioned classes (N-texture vs. 1-depth/1-texture) by using one depth image for each texture image, i.e., N-depth/N-texture [8] (see Figure 1.4). This approach has multiple advantages. First, as previously highlighted, the problem of occluded regions can be addressed by combining multiple reference images that cover all regions seen by the virtual camera. Second, the N-depth/N-texture representation format is compatible with different types of multi-view displays supporting a variable number of views. More specifically, because 3D geometry data is transmitted to the decoder, an arbitrary number of synthetic views corresponding to the display characteristics, can be interpolated. A final advantage is that the N-depth/N-texture representation format provides a natural extension to the 1-depth/1-texture representation format. Therefore, this approach allows a gradual transition from an already standardized technique (MPEG-C Part 3) to the next generation of 3D video systems. Because of these advantages, we have adopted the N-depth/N-texture representation format as the basis for conducting all experiments and studies through the complete thesis.

Figure 1.4 The N-depth/N-texture representation format combines N texture with N depth views.

Multi-view acquisition, compression and rendering problems addressed in this thesis

Acquisition problem

In a multi-view system, multiple cameras capture the same scene. In order to capture a 3D representation of the scene (using the N-depth/N-texture representation format), a signal is required that describes the geometric features in three dimensions As previously discussed, the depth of a pixel can be calculated by triangulating corresponding pixels across the views. By assigning a depth value to each pixel of the captured texture image and combining those depth values into an image, a depth image is created.

Corresponding pixels across the views are known as point-correspondences. Hence, in this thesis, the three-dimensional multi-view video acquisition step corresponds to the task of calculating multiple depth images by estimating point-correspondences across the multiple camera views. The calculation of depth by estimating point-correspondences is an ill-posed problem in many situations. For example, a change of illumination across the views increases the signal ambiguity while identifying the potentially corresponding points. Additionally, with multiple cameras, the internal settings like the contrast setting can vary, so that corresponding pixels show dissimilar intensity values. This results in an unreliable identification of the point-correspondences and thus in inaccurate depth values. Furthermore, specular reflection refers to the phenomenon that occurs when light is reflected in different directions with varying intensity. As a result, object surfaces appear differently depending on the viewpoint. Such a surface is known as a non-Lambertian surface. In this thesis, we assume that the 3D objects of the video scene do not change their appearance depending on the camera viewpoint, hence we assume Lambertian surfaces. Another problem that may occur in the scene is the appearance of texture-less regions. Specifically, it is difficult to identify corresponding pixels over a region of constant color, thereby resulting in inaccurate depth values. Moreover, in some cases, particular background regions may be visible from a given camera viewpoint but may not be visible from a different camera viewpoint. This problem is known as occlusion. In this case, it is not possible to identify point-correspondences across the views, so that the depth values (of the point-correspondences) cannot be calculated.

In this thesis, we have concentrated on a few specific problems dealing with multi-view system design, rather than addressing all of the above. Our aim is to design a depth estimation sub-system that can be efficiently combined with the multi-view depth compression sub-system and the image rendering sub-system. Specifically, considering the multi-view video coding framework, the depth estimation sub-system should:

• calculate an accurate depth of individual pixels,

• estimate depth images with smooth properties on the object surfaces so that a high compression ratio (of depth images) can be obtained,

• present sharp discontinuities along object borders so that a high rendering quality can be obtained,

• yield consistent depth images across the views so that the multi-view compression sub-system can exploit the inter-view redundancy (between depth views).

The last requirement is further detailed in the next section, since it is less evident than the first three requirements.

Compression problem

The transmission of an N-depth/N-texture multi-view video requires efficient compression algorithms. The intrinsic problem when dealing with a multitude of depth and texture video signals is the large amount of data to be transmitted. For example, an independent transmission of 8 views of a typical sequence such as the multi-view “Breakdancers” sequence, requires about 10 Mbit/s for the texture and 1.7 Mbit/s for the depth data (at a PSNR of 40 dB).² This example forms a typical situation of the specification of a multi-view sequence and its compression system. In this thesis, we aim at designing a compression system with the following characteristics.

• Spatial resolution: HD-ready to HD, hence 1000–1920 pixels per line and 768–1080 lines.

• Frame rate: 15 to 30 frames per second.

• Number of views: 2 to 10, depending on the application.

• Bit rate for depth: 10 to 50% of the total bit rate, depending on the desired rendering quality.

The above list does not express that multi-view video cannot be applied to other resolutions, frames and bit rates. It is merely intended to provide a quick outline of the video systems that will be elaborated in this thesis.

As many parts in the multi-view signal are correlated, this aspect could be exploited in the compression. In a typical multi-view acquisition system, multiple cameras are employed to capture a single scene from different viewpoints. By capturing a single scene from varying viewpoints, the multiple cameras capture objects with similar colors and textures across the views, thereby generating a highly correlated texture video. The correlation between the camera views is usually referred to as inter-view correlation. This correlation exists both for texture and depth signals. For each view, whether it is texture or depth, the succeeding frames have correlation over time, called temporal correlation. As temporal correlation within a single view is already exploited by the existing coding standards such as MPEG-2 and H.264/MPEG-4 AVC, by employing motion compensated transform coding. Let us now further discuss the inter-view correlation. The inter-view correlation can be exploited for compression, for example, with a predictive coding technique, as the neighboring views show most of scene from a different viewpoint. However, an accurate prediction of views is a difficult task. For example, illumination and constrast changes from view to view and additionally, the system has to deal with occlusions which is new information, and thus not correlated with a neighboring view. This is why it is thoroughly addressed in a specific chapter focusing on predictive inter-view coding.

In the compression system for multi-view video, we have concentrated on the following problems.

• Efficient compression for variable baseline-distances between cameras. The baseline-distances refer to the distances between cameras of the multi-view acquisition setup. However, considering inter-view correlation, multi-view video captured by an acquisition setup with a large baseline distance between the cameras has limited inter-view correlation. Therefore, an encoder is desired that adapts to the various baseline distances of the acquisition setup. One way that is exploited in this thesis, is to selectively predict regions from the multi-view images related to that baseline-distance.

• Low-delay random access to a selected view. An interesting feature of a free-viewpoint video system is the ability for users to quickly access an arbitrary selected view, i.e., random access to a selected view. To enable a user to render an arbitrary selected view of the video scene with an acceptable response time (computer graphics experts call this interactive frame-rate), low-delay random access is necessary. However, temporal and spatial inter-view coding creates dependencies between views during the encoding process, which deteriorates the random-access capabilities. Therefore, we aim at a coding system that facilitates random access with a reasonable response time as a design criterion.

• Efficient compression of depth images. To render synthetic views on a remote display, an efficient transmission and thus compression of the depth images is necessary. Previous work on depth image coding has used a transform-coding algorithm derived from JPEG-2000 and MPEG encoders. However, transform coders have shown a significant shortcoming for representing edges without deterioration at low bit rates. Perceptually, such a coder generates ringing artifacts along edges that lead to errors in the rendered images. Therefore, we aim at a depth image encoder that preserves the edges, so that a high-quality rendering can be obtained. A solution explored in this thesis is to exploit the special characteristics of depth images: smooth regions delineated by sharp edges.

• Efficient joint compression of texture and depth data such that the rendering quality is maximized. To perform an efficient compression of the N-depth/N-texture multi-view video streams, an efficient joint compression of both the texture and the depth data is necessary. Previously, the compression of such a data set has addressed the problem of texture and depth compression by coding each of the signals individually. However, the influence of texture and depth compression on 3D rendering was not incorporated in the coding experiments, so that the rendering quality trade-off was not well considered. We therefore aim at a method that optimally distributes the bit rate over the texture and the depth image, such that the 3D rendering quality is maximized.

Rendering problem

In general, rendering involves the read-out and presentation process of images. In a multi-view coding system, image rendering refers to the process of generating synthetic images.

In our case, synthetic images are rendered by combining the multiple texture images with their corresponding depth images. Over the past decade, image rendering has been an active field of research for multimedia applications [16]. However, limited work has addressed the problem of image rendering in a multi-view video coding framework. Specifically, it will be shown in this thesis that image rendering can be integrated into the multi-view coding algorithm, by employing the rendering procedure in a predictive fashion. When doing so, the quality of the rendered images should match the quality of other non-synthetic images. This implies that the rendering process should be of high quality, dealing with occlusions and the change of scene-sampling position when going from one view to the other. The latter aspect requires accurate texture pixel re-sampling. Summarizing, and more broadly speaking, there are two key aspects for rendering: visualization and compression. Both aspects can be simultaneously addressed when aiming at high-quality rendering. In this thesis, the rendering problem is discussed using the following requirements.

• In the prediction-based rendering algorithm that is related to the multi-view coding system, the rendering algorithm should synthesize high-quality images by accurate pixel re-sampling, and

• the rendering algorithm should correctly handle occluded pixels, so that even occluded pixels can be efficiently compressed at low bit rate.

Thesis outline: the multi-view video system

Besides the introduction and conclusion chapters (Chapter 1, Chapter 2 and Chapter 8), the core part of this thesis is divided into five chapters. Each individual chapter focuses on a sub-system of the proposed multi-view video system. Figure 1.5 shows the proposed system architecture, which is composed of a depth-estimation sub-system (Chapter 3), a multi-view texture and depth video coder/decoder (Chapter 5, 6 and 7), and a 3D-video rendering engine (Chapter 4). In the following, we outline each of these sub-systems.

Figure 1.5 Overview of the proposed multi-view video system that includes the acquisition of 3D video (depth estimation), the coding and decoding of the multiple texture and depth image sequences and the rendering sub-system.

A. 3D/multi-view video acquisition

Chapter 2 contains introductory material to specify the geometry of multiple views. We especially describe a method for calculating the internal and external parameters of the multiple cameras. This task is known as camera calibration. The principal result of the chapter is the specification of the projection matrix and its usage for depth estimation and image rendering.
Chapter 3 concentrates on the problem of acquiring a 3D geometric description of the video scene, i.e., depth estimation. At first, we focus on the problem of depth estimation using two views and present the basic geometric model that enables the triangulation of corresponding pixels across these two views. We review two calculation/optimization strategies for determining corresponding pixels: a local depth calculation and a one-dimensional optimization strategy. Second, we generalize the two-view geometric model for estimating the depth, using all multiple views simultaneously. Based on this geometric model, we propose a multi-view depth-estimation technique, based a one-dimensional optimization strategy that reduces the noise level in the estimated depth images and enforces consistent depth images across the views.

B. Multi-view depth image based rendering

Chapter 4 addresses the problem of multi-view image rendering. We commence with reviewing two different rendering techniques: a 3D image warping and a mesh-based rendering technique. We show that each of these two techniques suffers from, either low image rendering quality, or high computational complexity. To circumvent the aforementioned issues, we propose two image-based rendering algorithms: an alternative formulation of the relief texture algorithm and an inverse mapping rendering technique. Experimental comparisons with 3D image warping show an improvement in rendering quality of 3.8 dB for the relief texture mapping and 3.0 dB for the inverse mapping rendering technique.

C. Multi-view video coding

In the presented multi-view video system, the video coding blocks include the encoding and decoding of both the multi-view depth and texture video.
Chapter 5 addresses the problem of encoding the multi-view depth and texture video, using an extended version of a standard H.264/MPEG-4 AVC video encoder. The concept is based on exploiting the correlation between neighboring views. To this end, two view-prediction tools are used in parallel by the encoder: a block-based disparity-compensated prediction and a View Synthesis Prediction (VSP) scheme. Our encoder adaptively selects the most appropriate prediction scheme, using a rate-distortion criterion for an optimal prediction-mode selection. We present experimental results for several texture and depth multi-view sequences, yielding a quality improvement of up to 0.6 dB for the texture and 3.2 dB for the depth, when compared to solely performing H.264/MPEG-4 AVC disparity-compensated prediction. In this proposal, the use of the VSP scheme for multi-view depth encoding is original and particularly attractive because the prediction scheme does not rely on additional side information for prediction. To preserve random-access capabilities to any user-selected view, we employ a prediction structure that requires only two reference cameras.
Chapter 6 focuses on the compression of the depth signal. We present a novel depth image coding algorithm that concentrates on the special characteristics of depth images: smooth regions delineated by sharp edges. The algorithm models these smooth regions using piecewise-linear functions and sharp edges by a straight line. Since this approach is new and no alternative depth encoder was published at the time of this research, the proposed algorithm was compared with a JPEG-2000 encoder, which is the de-facto standard for digital cinema. A comparison with an encoder based on H.264/MPEG-4 AVC is also discussed. For typical bit rates (between 0.01 bit/pixel and 0.25 bit/pixel), experiments have revealed that the proposed encoder outperforms a JPEG-2000 encoder by 0.6-3.0 dB.

Chapter 7 discusses a novel joint depth/texture bit-allocation algorithm for the joint compression of texture and depth images. The described algorithm combines the depth and texture Rate-Distortion (R-D) curves to obtain a single R-D surface. This surface allows the optimization of the quantization parameters such that the rendering quality is maximized. Next, we discuss a hierarchical algorithm that enables a fast optimization by exploiting the smooth monotonic properties of the R-D surfaces. Experimental results show an estimated gain of up to 1 dB compared to a compression performed without joint bit-allocation optimization and using an encoder based on H.264/MPEG-4 AVC.

Contributions of this thesis

This section provides an overview of the scientific contributions along with the corresponding publication history, since most of the results have been published in conference proceedings or scientific journals.

Contributions to depth estimation

Depth estimation has been widely investigated, but we have added two contributions by adding smoothness constraints.

• Integration of a smoothness constraint for line consistency. We have proposed a smoothness constraint that enforces consistent depth between consecutive lines and we describe its integration into a simple one-dimensional optimization algorithm. This constitutes the first pass of the algorithm and results in one initial depth image for each view.

• Integration of a smoothness constraint for inter-view consistency. In a second pass, we have proposed a constraint that ensures consistent depth values across the views. This constraint is based on the re-projection of depth images (calculated at the first pass) onto the considered view as a means for improving the inter-view depth consistency. As a bonus, this re-projection method provides a simple solution for detecting noisy depth pixels.

The concept of integrating these smoothness constraints into a one-dimensional optimization algorithm was published in the Proceedings of the IEEE ICCE [17] and an elaborate description in the corresponding IEEE Transactions [18].

Contributions to image rendering

We propose two novel algorithms for rendering synthetic images using multiple depth and texture images.

• Novel formulation of the relief texture mapping. This novel specification has a formulation that matches with the geometry of multiple views. The proposed technique combines the two advantages of avoiding rendering artifacts (“holes”) in the synthetic image while simultaneously enabling an implementation on a standard Graphics Processor Unit architecture.

• Inverse mapping image rendering. We propose an inverse mapping rendering technique that allows a simple and accurate re-sampling of synthetic pixels. Additionally, the presented method provides a simple means for handling occlusions by an elegant, unambiguous construction of a single synthetic image from the two compositing neighboring views.

Preliminary results on image rendering were published in the Proceedings of the Symposium on Information Theory in the Benelux [19] and the new formulation of the relief texture rendering algorithm was published in the Proceedings of the SPIE SDA conference [20]. The inverse mapping is a new unpublished result of which a publication is under development.

Contributions to multi-view video coding

This part forms the most significant contribution of this thesis.

• Integration of a view-synthesis prediction algorithm into a multi-view depth and texture coder. The first contribution is the integration of an image rendering algorithm into a standardized H.264/MPEG-4 AVC video compression algorithm, to support predictive compression of multi-view video. We present a new coding tool that enables the compression of both multi-view texture images and also multi-view depth images. The rendering-based multi-view depth compression is completely new. This contribution has been published in the Proceedings of the IEEE ICIP [21] for texture multi-view coding and in the Proceedings of the SPIE SDA conference [22] for depth multi-view coding. Additionally, the impact of the view synthesis algorithm for predicting and encoding depth images was investigated and published in the Proceedings of the ACIVS conference [23].

• Depth coding with piecewise linear functions. The new algorithm models smooth regions in depth images with piecewise-linear functions and sharp edges by straight lines. Preliminary results were published in the Proceedings of 26th Symposium on Information Theory in the Benelux [24] and a fast method for estimating the model coefficients was published in the Proceedings of the SPIE VCIP conference [25]. A rate-distortion optimization of the encoder was published in the Proceedings of the EUSIPCO conference [26]. A complete description of the coding algorithm was published in the Proceedings of the SPIE SDA conference [20] and further improvements based on predictive coding of model coefficients were published in the Proceedings of the IEEE ICIP [27]. Due to the work of the author on depth image compression, a cooperation with the Fraunhofer-Institute for Telecommunications Heinrich-Hertz-Institut of Berlin was initiated and resulted in two joint publications in the Proceedings of the IEEE Conference on 3D-TV [28] and in the journal on Signal Processing: Image Communication [29].

• Joint bit-allocation for depth and texture multi-view coding. A third contribution is a novel algorithm that concentrates on the joint compression of depth and texture images. Instead of the conventional separated optimization of texture and depth, the proposed algorithm considers for the first time a joint optimization of both the rate and the distortion so that an optimal rendering quality is obtained. This work was published in the Proceedings of the Picture Coding Symposium [30] and obtained a Best Paper award nomination.

References